Содержание
Какие методы используют для расчета нагрузок
Для расчета нагрузки на профильную трубу пользуются:
- таблицами;
- математическими формулами;
- специальным онлайн калькулятором.
Применяем таблицы
При применении первого метода нужно сопоставление физических характеристик трубы, которая будет применяться для сооружения системы, с табличными данными. Для этого берут значения величин из таблиц 1 или 2, в зависимости от типа профиля.
Таблица 1. Нагрузки для стояков квадратного сечения
| Сечение, мм |
Максимально возможная масса, кг | |||
| Длина пролета, м | ||||
| 1 | 2 | 4 | 6 | |
| 40х40х2 | 709 | 173 | 35 | 5 |
| 50х50х2 | 1165 | 286 | 61 | 14 |
| 60х60х3 | 2393 | 589 | 129 | 35 |
| 80х80х3 | 4492 | 1110 | 252 | 82 |
| 100х100х4 | 9217 | 2283 | 529 | 185 |
| 140х140х4 | 19062 | 4736 | 1125 | 429 |
Таблица 2. Нагрузки для стояков прямоугольного сечения
(для вычислений используют длинную сторону)
| Сечение, мм |
Максимально возможная масса, кг | |||
| Длина пролета, м | ||||
| 1 | 3 | 4 | 6 | |
| 50х25х2 | 684 | 69 | 34 | 6 |
| 60х40х3 | 1255 | 130 | 66 | 17 |
| 80х40х3 | 2672 | 281 | 146 | 43 |
| 80х60х3 | 3583 | 380 | 199 | 62 |
| 100х50х4 | 5489 | 585 | 309 | 101 |
| 120х80х3 | 7854 | 846 | 455 | 164 |
Эти таблицы имеют данные о максимально допустимых массах. При таком воздействии на профиль труба не разрушится, а лишь согнется.
В связи с этим, на практике выбирается деталь прямоугольного или квадратного сечения, запас прочности которой был бы большим от минимального хотя бы в 2 раза.
Преимущества табличного метода
Табличный метод отличается высокой точностью. Для его применения нужно обладать информацией о видах опор, способах фиксации на них профилей, типах нагрузок.
Кроме этого, для полных расчетов нагрузок необходимо иметь данные о:
- моментах инерции профильной прямоугольной или квадратной трубы, значение которых можно взять из таблиц, начиная от сечений 15х15х1 5 и оканчивая 100х100х4 и выше;
- длине пролетов;
- величине тяжести на каждый стояк;
- коэффициентах модулей упругости (взять из СНиП).
Масса 1 м.п. профиля 15х15х1,5 составляет 0,606 кг. Исходя из этого, можно провести соответствующие вычисления.
После этого переходим к специальным формулам, то есть, к математическому методу. В соотношениях показано, как связаны между собой данные физические величины, как найти неизвестную величину, имея 2 или больше известных параметра и пр.
А может лучше калькулятором?
Быстрее всего можно провести расчеты с применением калькулятора. Особенность такой программы состоит в том, что необходимо ввести нужные параметры, характеристики изделий, линейные размеры, иные свойства будущей конструкции. В конце онлайн калькулятор выдаст расчет нагрузки профильной трубы для заданных параметров.
Важно! Для расчета нагрузок нужно пользоваться специальными онлайн калькуляторами, которые размещены на сайтах надежных компаний. Важно! Лучше всего воспользоваться услугами лиц, которые знакомы с ГОСТами, разбираются в строительстве, сопромате, имеющие опыт работы с аналогичными программами
Что в первую очередь рассчитывают при помощи формул
Вычисляют многие параметры.
Чаще других ищут:
- Допустимый уровень напряжения при изгибах. Используется формула
Р= M/W,
где Р – возможное напряжение при изгибе,
М – значение изгибающего момента силы,
W – механическое сопротивление. - Требуемое сечение стояка:
F = N/R,
где F – необходимая площадь сечения (см²),
N – действующая масса (кг),
R – значение сопротивления металла при деформациях, соответственно пределу текучести (кг/см²).
Значения физических величин можно отыскать в специальных таблицах.
Онлайн калькулятор для расчёта стойки (колонны) из стального проката
Укажите вид проката Круг Квадрат Полоса Шестигранник Материал проката Вид и назначение стоек Если Вашего материала нет в таблице, но Вам известно расчётное сопротивление этого материала, ведите его значение в это поле (кг/см2):
Введите параметры для расчёта
| Длина стойки (колонны) L, м | Размер D или Dv, или A, мм |
| Размер B, мм | Нагрузка на стойку P, кг |
Логика онлайн расчета на прочность и устойчивость стойки из стального проката
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) рассчитывая на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P / Fp * Ry * Yc <= 1
- где P – действующая нагрузка.
- Fp – площадь поперечного сечения колонны.
- Ry – подсчетное сопротивление материала (стали колонны), выбирается по таблице В5 Приложения “В” того же СНиПа.
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi * Fp * Ry * Yc <= 1
где Fi – коэффициент продольного изгиба центрально – сжатых элементов.
Коэффициент Fi введён в качестве компенсации возможности некоторой не прямолинейности колонны, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки.
Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г., исходя из гибкости колонны и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет вычисления, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечн. сечения, в частности радиуса инерции:
Lambda = Lr / i
- здесь Lr – расчётная длина стержня,
- i – радиус инерции поперечного сечения стержня (колонны).
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где I – момент инерции, Fp – его площадь.
Lr (расчётная длина) определяется как Mu*L; здесь L – длина стойки, а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu=2;
- “заделка-заделка” – Mu = 0.5;
- заделка – шарнир” – Mu = 0.7;
- “шарнир – шарнир” – Mu = 1.
Следует иметь ввиду,что при наличии у формы поперечн. сечения 2-ух радиусов инерции (например, у прямоугольника), при вычислении Lambda используется меньший.
Для их использования необходимо сделать выбор в таблице онлайн калькулятора “Вид, назначение стоек”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стоики (Ry) и условий её работы (Yc).
Предельная гибкость, устойчивость и прочность стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
Изменения, внесенные в работу калькулятора
Исправления, внесенные от 8 сентября 2018 года включают:
1.добавление проверки локальной устойчивости стенок либо полок в двутавре, или швеллере, или уголке, также металлического профиля.
Исправления, внесенные от 2 декабря 2018 года, включают:
1.исправление расчетного параметра сопротивления деревянного материала на сжатие в разделе СП под названием ”Деревянные конструкции».
2.исправление коэффициентов расчетного значения по длине, применяемые для материала из дерева.
3.исправление замечаний, отображающих итоговые расчеты.
Вычисления максимального уровня нагрузки
Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей
Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах
Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.
В результате вычисления максимальной нагрузки получаем следующий результат: q=(60+250+75)*0,6+18=249 кг/м.
Когда значение получено, можно переходить к расчету максимального прогиба.
Нагрузка на трубы круглого сечения
Применение
Круглые трубы можно встретить в любом месте. Опоры, стойки, колонны, емкости – это далеко не полный перечень использования обечаек (обечайка – металлический лист цилиндрической формы без торцов).
Кольцевой трубный профиль можно встретить при прокладке водо-, нефте-, газопроводов как в быту, так ив промышленных масштабах. Они – отличный материал для столбиков ограждений, ворот, калиток.
Благодаря наличию замкнутого контура, круглая труба обладает существенным преимуществом в сравнении со швеллерами, уголками аналогичных линейных параметров.
В результате деления первого параметра на второй, получил искомую прочность. После сравнения полученного параметра с допускаемым значением, взятого с таблицы, делают вывод о том, можно ли такую нагрузку давать на конкретный стояк, или нельзя.
Если число будет меньше допускаемого, то все хорошо. Но тут есть одно но: вычисления справедливые для растягивания, а не для сжатия.
Пользуемся калькулятором
Для варианта со сжатием круглой стойки, можно провести необходимые расчеты с использованием онлайн калькулятора.
Сначала необходимо ознакомиться с дополнительными понятиями. Сюда относят:
- Потерю общей устойчивости.
Проверка потери нужна для избегания огромных потерь иного типа. - Потерю местной устойчивости.
Речь идет о более раннем «заканчивании» жесткости стенок стояка при действии нагрузки на обечайку. Иначе говоря, труба начинает заламываться вовнутрь, а сечение круглого вида превращается в профиль неправильной криволинейной формы, что ведет к потере устойчивости.
Использование Excel
Существует специальная программа в Excel комплексной проверки расчета стояков относительно устойчивости и прочности. Основу данной программы составляют данные ГОСТа 14249 89. С ее помощью можно вычислить максимальную нагрузку на круглую трубу, а также усилия общего характера на обечайку круглого сечения.
В интернете можно часто встретить такие вопросы: «Какую нагрузку выдерживает круглая труба длиной 3, 4, 6 метров? Как это вычислить с помощью онлайн калькулятора? Можно ли это сделать самостоятельно?»
На эти и другие вопросы постараемся дать подробный ответ. Лучшим объяснением будет практический расчет величины вертикальной нагрузки на круглую трубу. Для примера, возьмем вертикальный круглый стояк диаметром 57 мм длиной 3 метра (чаще всего используется для обустройства навесов, гаражей, иных сооружений) и вычислим, какую нагрузку труба сможет выдержать.
Какие данные нужны
Алгоритм работы с программой состоит в следующем:
- Сначала нужно открыть ГОСТ 14249 89, из которого необходимо выписать первых 5 исходных значений. Для быстрого отыскания параметров воспользоваться примечаниями к каждой ячейке.
- Заполнить ячейки D8, D9, D10, вписывая в них линейные параметры стояков.
- В ячейки от D11 до D15 внести возможные нагрузки.
Важно! Если на обечайку будет действовать внутреннее избыточное давление, то значение наружного давления равняется нулю. Аналогично: при воздействии на стояк внешнего избыточного давления, параметр внутреннего давления также будет равным нулю
Важно! Помните, что примечания к каждой ячейке в столбце «Значение» содержат в себе ссылку номеров нужной формулы, необходимой таблицы или чертежа из ГОСТа 14249 89
Что получилось в результате
Нужно не только уметь пользоваться программой, но также уметь объяснить полученные результаты.
Необходимо сопоставить отношение действующей нагрузки к допускаемой: при получении числа, большего за единицу, труба – перегруженная. В противном случае – заданный вес стояк выдержит, при условии, что расчет нагрузки на трубу круглого сечения проведен правильно.
Важно! Пользователь должен увидеть значение суммарного влияния всех действующих сил и давлений
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
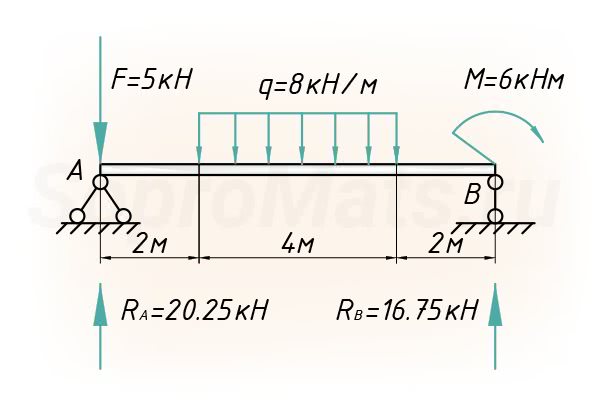
Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\
\
Записываем уравнение метода начальных параметров для сечения C:
\
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
\
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:
Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:
Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:
Все сосредоточенные моменты нужно умножать дробь:
\
Все сосредоточенные силы нужно умножать дробь:
\
Начало и конец распределенных нагрузок нужно умножать на дробь:
\
Откуда такие цифры и степени взялись? Все эти вещи вытекают при интегрировании дифференциального уравнения упругой линии балки, в методе начальных параметров все эти выводы опускаются, то есть он является как бы упрощенным и универсальным методом.
Формулы прогибов
С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:
\
Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:
\
Упрощаем уравнение:
\
Выражаем угол поворота:
\
Подставляем это значение в наше первое уравнение и находим искомое перемещение:
\
Профильная труба и способы использования
Профиль можно применять в сборке практически любых конструкций, промышленного, коммерческого и бытового назначения. В быту ее часто используют для сборки систем хранения вещей, в качестве аквариумной подставки, для навесов на балконе или веранде. На профиле может удерживаться мебель: стол, барная стойка, телевизионная подставка, поручни для занятий. Профиль часто применяется в коммерческом строительстве, из него собирают лестницы, различные легконесущие конструкции для террас, навесов, подиума и сцены.

Разновидности профильных труб
Список можно продолжить, профиль подходит для различных решений, поэтому часто привлекает мастеров, использующих его в строительстве и дизайне. Чаще всего из трубы изготавливают опору под барную стойку, держатели для шкафа купе или аквариумную подставку. Наиболее щепетильно нужно отнестись к подставке для аквариума и учесть постоянно оказываемую нагрузку. В зависимости от этого параметра выбирается материал для изготовления.

Подставка под аквариум из проф трубы
Расчет максимального прогиба для балки с двумя опорами
В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Выбираем типоразмер трубы для монтажа забора из профлиста
Нужно подобрать такую трубу, чтобы ее прочность на изгиб перекрывала момент, равный 291,75 кгс•м. Для этого осталось вычислить максимальный изгибающий момент балки:
М = σW/1000
- σ — Предел текучести материала (кгс/мм2), для стали Ст1пс и Ст10 (материал труб стандартного качества) составляет 20-21 кгс/мм2.
- W – момент сопротивления сечения (мм3).
- 1000 – цифра для перевода измерений из миллиметров в метры.

Момент осевого сопротивления при изгибе
Для круглой трубы
W=π(D4-d4)/32D
На основании несложных вычислений получаем разрушающие моменты для существующих типов труб круглого сечения.
| Внешний диаметр трубы, мм | Толщина стенки, мм | Разрушающий момент, кгс·м |
| 60 | 2 | 102,28 |
| 60 | 3 | 145,85 |
| 76 | 2,5 | 205,41 |
| 76 | 3 | 241,62 |
| 76 | 3,5 | 276,31 |
| 76 | 4 | 309,53 |
| 89 | 3 | 337,19 |
| 89 | 3,5 | 386,74 |
| 89 | 4 | 434,52 |
Для квадратной трубы
W=(H4-h4)/6H
Разрушающие изгибающие моменты труб квадратного сечения:
| Наружный размер трубы, мм | Толщина стенки, мм | Разрушающий момент, кгс·м |
| 60 | 2 | 173,64 |
| 60 | 2,5 | 211,63 |
| 60 | 3 | 247,61 |
| 60 | 3,5 | 281,64 |
| 60 | 4 | 313,8 |
| 80 | 3 | 457,23 |
| 80 | 4 | 586,92 |
Что имеем?
Глядя на таблицы, можно определить, что для установки забора из профнастила с шагом и высотой по два метра, подойдет квадратная труба, начиная с размера 60х4 мм, или круглая – начиная с 76х4 мм. Все рекомендуемые типоразмеры выделены зеленым цветом. Чем шире пролеты и выше ограждение, тем прочнее должна быть опора.
Дизайнерско-эстетические предпочтения не должны быть основополагающими при выборе круглой или квадратной трубы. Не стоит забывать и ряд инженерно-экономических критериев.

Предварительные соображения
Калькулятор предусматривает расчёт балок из некоторых видов проката на изгиб и прогиб для различных схем их крепления и нагрузки. Нагрузка балок может быть распределённой (“q” на схемах 3, 4, 5, 9, 15 и других) или сосредоточенной (“P” на схемах 1, 2, 6, 7, 8 и других.)
Крепление балок может быть:
- консольным с жесткой заделкой одного из концов (например, схемы 1, 2, 3 и другие);
- “заделка – заделка”, когда оба конца балки жестко защемлены (заделаны), схемы 6, 7, 8, 9;
- “шарнир – шарнир”, (схемы 12, 13, 14, 15 и другие), причём левый шарнир неподвижный а правый подвижный;
- “заделка – шарнир”, (схемы 9, 10, 11 др.)
Жесткая заделка балки предотвращает ее поворот и перемещение в любом направлении. Неподвижный шарнир допускает только поворот балки в месте крепления в вертикальной плоскости. Подвижный шарнир допускает поворот балки в месте крепления в вертикальной плоскости и перемещение вдоль её собственной оси. Эти перемещения весьма незначительны и являются следствием деформации балки под нагрузкой.
Основным видом этой деформации является её прогиб, величина которого наряду с приложенной к балке нагрузкой зависит также от ее длины, размеров её поперечного сечения и физических характеристик материала, в данном случае от его модуля упругости (“E”).
Из размерных характеристик поперечного сечения балки для расчёта прогиба используется момент инерции сечения (“I”); величина прогиба зависит также от положения проверяемой точки балки относительно опор. Допустимая величина прогиба балок определяется их назначением и местом в строительных конструкциях и регламентируется соответствующим СНиП; в легких случаях она не должна превышать 1/120 – 1/250 длины балки.
В связи с чем настоятельно рекомендуем проверять результаты расчета на допустимость после использования калькулятора.
С помощью нашего онлайн калькулятора вы сможете рассчитать:
- Допускаемое напряжение при изгибе (кг/см2).
- Максимальный изгибающий момент (кг/см).
- Момент сопротивления изгибу (см3).
- Осевой момент инерции поперечного сечения (см4).
- Максимальный прогиб (см).
- Расчётное напряжение при изгибе (кг/см2).
Построить дом невозможно без использования разделяющих перекрытий. Одно из них отделяет дом от наружного пространства снизу, второе – сверху. На них монтируются пол, и потолок здания, производится утепление. Горизонтальные перемычки должны выдерживать собственный вес, а также переносить нагрузки от мебели, оборудования и людей в здании.
Расчет внецентренно-сжатой колонны.
Тут конечно же возникает вопрос: а как рассчитать остальные колонны, ведь нагрузка к ним будет приложена скорее всего не по центру сечения? Ответ на этот вопрос сильно зависит от способа крепления навеса к колоннам. Если балки навеса будут жестко крепиться к колоннам, то при этом будет образована достаточно сложная статически неопределимая рама и тогда колонны следует рассматривать как часть этой рамы и рассчитывать сечение колонн дополнительно на действие поперечного изгибающего момента, мы же далее рассмотрим ситуацию когда колонны, показанные на рисунке 1, соединены с навесом шарнирно (колонну, обозначенную красным цветом, мы больше не рассматриваем). Например оголовок колонн имеет опорную площадку — металлическую пластину с отверстиями для болтового крепления балок навеса. По разным причинам нагрузка на такие колонны может передаваться с достаточно большим эксцентриситетом:
Рисунок 2. Эксцентриситет приложения сосредоточенной нагрузки к колонне из-за прогиба балки навеса.
Балка, показанная на рисунке 2, бежевым цветом, под воздействием нагрузки немного прогнется (почему это произойдет, обсуждается отдельно) и это приведет к тому, что нагрузка на колонну будет передаваться не по центру тяжести сечения колонны, а с эксцентриситетом е и при расчете крайних колонн этот эксцентриситет нужно учитывать. Более точное определение эксцентриситетов зависит от жесткости колонны и балки, но мы в данном случае не будем учитывать жесткости и для надежности примем максимально неблагоприятное значение эксцентриситета. Случаев внецентренного нагружения колонн и возможных поперечных сечений колонн существует великое множество, описываемое соответствующими формулами для расчета. В нашем случае для проверки сечения внецентренно-сжатой колонны мы воспользуемся одной из самых простых:
(N/φF) + (Mz/Wz) ≤ Ry (3.1)
Т.е. предполагается, что внецентренное нагружение имеется только относительно одной оси.
В данном случае, когда сечение самой нагруженной колонны мы уже определили, нам достаточно проверить, подходит ли такое сечение для остальных колонн по той причине, что задачи строить сталелитейный завод у нас нет, а мы просто рассчитываем колонны для навеса, которые будут все одинакового сечения из соображений унификации.
Что такое N, φ и Ry мы уже знаем.
Формула (3.1) после простейших преобразований, примет следующий вид:
F = (N/Ry)(1/φ + ez·F/Wz) (3.2)
так как максимально возможное значение изгибающего момента Мz = N·ez, почему значение момента именно такое и что такое момент сопротивления W, достаточно подробно объясняется в отдельной статье.
Сосредоточенная нагрузка N на колонны, обозначенные на рисунке 1 синим и зеленым цветом, составит 1500 кг. Проверяем требуемое сечение при такой нагрузке и ранее определенном φ = 0.425
F = (1500/2050)(1/0.425 + 2.5·3.74/5.66) = 0.7317·(2.353 + 1.652) = 2.93 см2
Кроме того, формула (3.2) позволяет определить максимальный эксцентриситет, который выдержит уже рассчитанная колонна, в данном случае максимальный эксцентриситет составит 4.17 см.
Требуемое сечение 2.93 см2 меньше принятого 3.74 см2, а потому квадратную профильную трубу с размерами поперечного сечения 50х50 мм с толщиной стенки 2 мм можно использовать и для крайних колонн.
Примечание: Вообще-то изгибающий момент от эксцентриситета в наиболее опасном сечении, расположенном примерно посредине высоты колонны, будет в 2 раза меньше, соответственно и требуемая площадь сечения тоже будет немного меньше. Но как я уже говорил, при выполнении расчета не специалистом дополнительный запас по прочности никогда не помешает. К тому же в данном случае мы все равно принимаем большую площадь сечения из конструктивно-эстетических соображений.
Примеры расчета стропил и обрешетки
Внимание: в текст статьи были внесены некоторые изменения с целью упрощения процедуры расчета
Дано:
Планируется такой себе двухэтажный домик 8х10 м, высота этажа 3 м (с учетом междуэтажных перекрытий). Место строительства – Московская область. Дом с пятью несущими стенами: 4 наружные и одна внутренняя, толщина наружных стен – 0.51 м, толщина внутренней стены – 0.38 м. Кровля – волнистые асбестоцементные листы. Стропильная система – двускатная кровля с опорными стойками по центральной несущей стене, шаг стропил – 1 м, обрешетка – доски необрезные толщиной 25 мм. Чердачное помещение – нежилое.
Примечание: Для большей надежности лучше сделать сплошной настил и дополнительную гидроизоляцию рубероидом перед укладкой шифера, но ограничимся расчетом бюджетного варианта.
Общие сведения по результатам расчетов
-
Общая длина ростверка
— Периметр фундамента, с учетом длины внутренних перегородок. -
Площадь подошвы ростверка
— Соответствует размерам необходимой гидроизоляции. -
Площадь внешней боковой поверхности ростверка
— Соответствует площади необходимого утеплителя для внешней стороны фундамента. -
Общий Объем бетона для ростверка и столбов
— Объем бетона, необходимого для заливки всего фундамента с заданными параметрами. Так как объем заказанного бетона может незначительно отличаться от фактического, а так же вследствие уплотнения при заливке, заказывать необходимо с 10% запасом. -
Вес бетона
— Указан примерный вес бетона по средней плотности. -
Нагрузка на почву от фундамента в местах основания столбов
— Нагрузка на почву от веса фундамента в местах основания столбов/свай. -
Минимальный диаметр продольных стержней арматуры
— Минимальный диаметр по СНиП, с учетом относительного содержания арматуры от площади сечения ленты. -
Минимальное кол-во рядов арматуры ростверка в верхнем и нижнем поясах
— Минимальное количество рядов продольных стержней в каждом поясе, для предотвращения деформации ленты под действием сил сжатия и растяжения. -
Минимальный диаметр поперечных стержней арматуры (хомутов)
— Минимальный диаметр поперечных и вертикальных стержней арматуры (хомутов) по СНиП. -
Минимальное кол-во вертикальных стержней арматуры для столбов
— Количество вертикальных стержней арматуры на каждый столб/сваю. -
Минимальный диаметр арматуры столбов
— Минимальный диаметр вертикальных стержней для столбов/свай. -
Шаг поперечных стержней арматуры (хомутов) для ростверка
— Шаг хомутов, необходимых для предотвращения сдвигов арматурного каркаса при заливке бетона. -
Величина нахлеста арматуры
— При креплении отрезков стержней внахлест. -
Общая длина арматуры
— Длина всей арматуры для вязки каркаса с учетом нахлеста. -
Общий вес арматуры
— Вес арматурного каркаса. -
Толщина доски опалубки
— Расчетная толщина досок опалубки в соответствии с ГОСТ Р 52086-2003, для заданных параметров фундамента и при заданном шаге опор. -
Кол-во досок для опалубки
— Количество материала для опалубки заданного размера.
Расчет опалубки колонн
При заливке колонн используется специально собранная опалубочная система. Это одноразовые комплексы или многоразовые сборные конструкции. Использование щитовых форм позволяет получить колонны с сечением в форме прямоугольника или квадрата. При формировании круглых колонн нередко применяются картонные формы.
Чтобы выполнить расчет опалубки колонн необходимо знать высоту конструкции, длину и ширину. Само собой, при постройке круглых элементов необходима информация о диаметре.
Чтобы получить точный расчет, обратитесь к консультантам компании Робуд. Опытные менеджеры проведут скрупулезные вычисления всех составляющих конструкции для создания высоконадежной опалубки.






